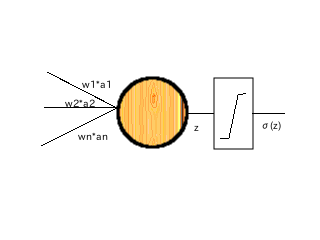
パーセプトロン
パーセプトロンの基本構造
パーセプトロンとは、n本の入力と1本の出力を持つ関数と考えることができます。
n本の入力は最初に重みwとの内積が計算され、バイアスbを加算した出力zに対し非線形で単調増加(後ほど導入する誤差逆伝搬法では更に1階微分可能な)な関数をかました形をしています。
Z の領域 (-∞,+∞) ですが、出力関数の出力を[0,1)にすることが可能です。
よく使用されるのがシグモイド関数とソフトマックス関数です。
シグモイド関数は以下のような形をしています。
\[
\sigma(z) = \frac{1}{1 + e^{-z}}
\]
ソフトマックス関数は出力が n 本ある場合の出現率を決めるような式で、以下のように定義されます。
\[
softmax(z_k) = \frac{e^z_k}{\sum_i e^z_i}
\]
余談ですが、この式の評価は途中で大きな値が発生して∞や NaN が発生するのを防止するため、以下のように変形するのが通例です。
\[
softmax(z_k) = \frac{e^{z_k - argmax_j z_j}}{\sum_i e^{z_i - argmax j z_j}}
\]
出力を[0, 1)にとると出現確率と解釈することが可能で、この記事では0.9以上なら出現、0.9未満なら出現しないと解釈することにします。
パーセプトロンでは AND, OR, NOT などが実現できることが知られています。
一方線形分離できない XOR は実現できません。(2つパーセプトロンを縦列するとできるようになります。)
実際に作ってみると、
| w1 | w2 | b | 実現するロジック |
| 1.1 | 1.1 | 0.1 | AND |
| -2.6 | 0 | 0.0 | NOT |
| 2.6 | 2.6 | 0.0 | OR |
| -1.0 | -1.0 | 2.3 | NOR |
となります。
パーセプロトロンのパラメータ w, b には任意性が残されていることに注意してください。
上記は唯一の解ではありません。
w, b の自動計算はできないのか?
入力と出力の組から w, b を推定する逆問題を考えます。
(以降、出力は k = 1...K 個あるとします。)
まず、損失関数(loss function)を導入します。入力値 \(x_i\) と教師ラベル \(y_i\) に対し、損失関数 \(L\) を
\[
L = L(\sigma(z_1), y_1; \cdots ; \sigma(z_N), y_N)
\]
と定義します。
よく使用されるのは二次損失関数
\[
L = \frac{1}{2 N} \sum^N_i||\sigma(z_i) - y_i||^2
\]
です。学習速度を上げるために交差エントロピー
\[
L = -\frac{1}{N} \sum^N_i \sum^K_k [y_{ik} ln(\sigma(z_{ik})) + (1 - y_{ik}) ln(1 - \sigma(z_{ik})]
\]
もよく使用されます。
損失関数を最小化する時の十分条件は \(L\) の全微分 \( \Delta L\) が 0 であることです。
もし全微分が 0 でなかったら各項の微分に対して逆符号方向に少しだけ動かすと全微分の絶対値をより小さくすることができる可能性があります。
\[
w_{jk} \leftarrow w_{jk} - \eta \frac{\partial L}{\partial w_{jk}}
\]
\[
b_k \leftarrow b_k - \eta \frac{\partial L}{\partial b_k}
\]
\( \eta \) は小さな正の値で学習率と呼ばれます。またこのようにパラメータを更新して最適解を求める方法を最急降下法と呼びます。
さて、通常サンプル数は1万以上あり、全てのサンプルについて上記の計算を行うのは効率的ではありません。
そこで、母集合から数百個程度の子集合を作り、それに対して最急降下法を適用してパラメータを決めることを考えます。
このとき、子集合の選択が完全にランダムならば子集合の選択を繰り返すことで、パラメータ値は母集合のパラメータ値に近づいていくことが期待されます。
このアルゴリズムを確率的最急降下法と呼びます。
損失関数が \(L = \alpha \sum L(\sigma(z_i), y_i) \) と書ける場合、微分 \( \partial L / \partial w_{jk}, \partial L / \partial b_k \) についてもう少し計算することができます。
まず微分の線形性から損失関数の係数(およびバイアス)に関する微分は、部分和に現れる \( L \) に関する微分の和に等しくなります。合成関数の微分に関する法則から、
\[
\frac{\partial L}{\partial w_{jk}} = \alpha \sum^n_i \sum^K_{k'} L'(s_{ik'}) \sigma'(z_{ik'}) \frac{\partial z_{ik'}}{\partial w_{jk}}
\]
ここで \( z_{ik'} = \sum_j x_{ij} w_{jk'} + b_k \) であることから、
\[
\frac{\partial L}{\partial w_{jk}} = \alpha \sum^n_i L'(s_{ik}) \sigma'(z_{ik}) x_{ij}
\]
\[
\frac{\partial L}{\partial b_k} = \alpha \sum^n_i L'(s_{ik}) \sigma'(z_{ik})
\]
が得られます。\( L \) が二次損失出関数である場合は \( L'(s_{ik}) = s_{ik} - y_k \)、また出力関数としてシグモイド関数を使用すると \( \sigma'(x) = \sigma(x) (1 - \sigma(x)) \) なので、係数の微分が簡単に計算できます。
アルゴリズム
以上を踏まえて、アルゴリズムを実装したクラス SimpleNet を java 風に記述すると、以下のようになります。
準備
// 損失関数
public interface ILossFunction {
public double deriv(double x, double y);
}
// 二次損失関数
public class QuadLossFunction implements ILossFunction {
@Override
public double deriv(double x, double y) {
return x - y;
}
}
// シグモイド関数
public static double sigmoid(double x) {
return 1.0 / (1.0 + Math.exp(-x));
}
public class SimpleNet {
// cache for backward propagation calculatiions
protected double[][] s;
protected double[][] in;
protected final double eta;
protected final int samplen, inn, outn;
private final ILossFunction loss;
private final Random rand;
private double[][] dw;
private double[] db;
// public members
public double[][] w;
public double[] b;
public SimpleNet(int samplen, int inn, int outnn, double eta) {
this.samplen = samplen;
this.inn = inn;
this.outn = outn;
this.eta = eta;
this.loss = new QuadLossFunction();
this.in = new double[inn];
this.s = new double[samplen][outn];
this.rand = new Random();
// public members
this.w = new double[inn][outn];
this.b = new double[outn];
// derivative counter part
this.dw = new double[inn][outn];
this.db = new double[outn];
}
public void initailizeWB() {
// set dw, db to zeros
}
// 後で説明します
public void initialize();
public double[][] forward(double[][] xin, int[] samples);
public void backPropagate(double[][] xin, double[][] labels, int count, int nset, int nchild);
protected void backPropagate(double[][] xin, double[][] labels, int nset, int[] samples);
public void backPropagate(double[][] xin, double[][] labels, int[] samples);
}
初期化
w は[-1.0, 1.0]の一様乱数で初期化します。b はゼロにして置きます。
public void initialize() {
IntStream.range(0, K).forEach(k->{
IntStream.range(0, n).forEach(j->{
w[j][k] = 2.0 * rand.nextDouble() - 1.0;
});
b[k] = 0.0;
});
}
順伝搬
線形和を取り、シグモイド関数を通します。
結果を後で誤差逆伝搬法を適用するために保存します。
// 入力は xin[N][K] あるものとする
// samples は子集合の index 集合とする
// 結果は r[n][K] に返される
public double[][] forward(double[][] xi, int[] samples) {
double[][] r = new double[samples.length][outn];
in = xin;
IntStream.range(0, outn).forEach(k->{
IntStream.range(0, samples.length).forEach(i->{
double z = IntStream.range(0, inn)
.mapToDouble(j->xin[samples[i]][j] * w[j][k])
.sum();
z += b[k];
r[i][k] = sigmoid(z);
s[samples[i]][k] = r[i][k];
});
});
return r;
}
逆伝搬
逆伝搬は3つのメソッドで構成します。
- 確率的最急降下法のためのサンプリング
- 子集合に対して確率的最急降下法の繰り返しループ
- 確率的最急降下法自身の実装
まず、確率的最急降下法を行うために母集合からサンプリングして子集合を作ります。
子集合に対して backPropagate(xin, labels, nset, samples) を適用していきます。
public void backPropagate(double[][] xin, double[][] labels, int count, int nset, int nchild) {
int[] samples = new int[nchild];
IntStream.range(0, count).forEach(n->{
IntStream.range(0, nchild).forEach(i->{
samples[i] = rand.nextInt(samplen);
});
backPropagate(xin, labels, nset, samples);
});
}
子集合に対して最急降下法を nset 回適用し、 \( \Delta L = 0 \) となる点を求めていきます。
protected void backPropagte(double[][] xin, double[][] labels, int nset, int[] samples) {
IntStream.range(0, nset).forEach(m->{
backPropagate(xin, labels, samples);
});
}
一番下のメソッドでは最急降下法を実装します。
public void backPropagate(double[][] xin, double[][] labels, int[] samples) {
// clear dw, db
initializeWB();
// calculate the RHS of the stochastic steepest descent method
IntStream.range(0, outn).forEach(k->{
IntStream.range(0, inn).forEach(j->{
double d = IntStream.range(0, samples.length)
.map(i->samples[i])
.mapToDouble(i->{
loss.deriv(s[i][k], labels[i][k])
* s[i][k] * (1.0 - s[i][k])
* xin[i][j]
}).sum();
dw[j][k] += d / (double)samples.length;
d = IntStream.range(0, samples.length)
.map(i->samples[i])
.mapToDouble(i->{
loss.deriv(s[i][k], labels[i][k])
* s[i][k] * (1.0 - s[i][k])
}).sum();
db[k] += d / (double)samples.length;
});
});
// add deltas
IntStream.range(0, outn).forEach(k->{
IntStream.range(0, inn).forEach(j->{
w[j][k] += dw[j][k];
});
b[k] += db[k];
});
}
Copyright (c) 2017-2019 by TeqStock.tokyo